[Cracking Coding Problems] Logical Puzzles

Posted Nov 25, 2024 Updated Nov 27, 2024

By Joe 11 min read

Basketball

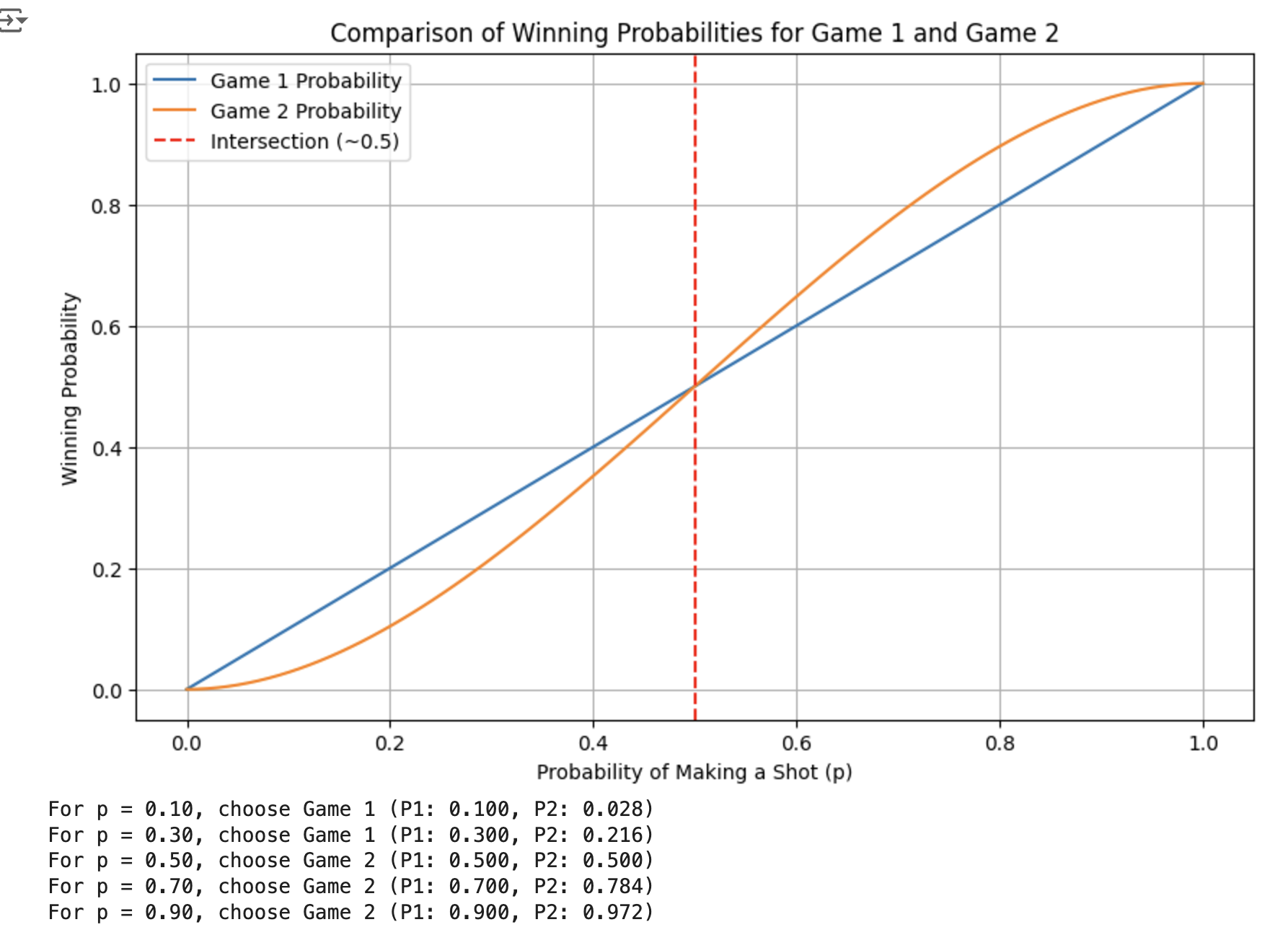
You have a basketball hoop and someone says that you can play one of two games.
- Game 1: You get one shot to make the hoop.
- Game 2: You get three shots and you have to make two of three shots.
If p is the probability of making a particular shot, for which values of p should you pick one game or the other?

Approach

Calculate probability with the probability mass function of a binomial distribution
\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]
- P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
Game1 : P(game1) = p
Game 2 : P(X = 2) + P(X = 3)

Prerequisite

Probability

Python

  
import numpy as np
import matplotlib.pyplot as plt

def game1_probability(p):
    return p

def game2_probability(p):
    return 3 * p**2 * (1 - p) + p**3

p_values = np.linspace(0, 1, 1000)
game1_probs = game1_probability(p_values)
game2_probs = game2_probability(p_values)

# plot
plt.figure(figsize=(10, 6))
plt.plot(p_values, game1_probs, label="Game 1 Probability")
plt.plot(p_values, game2_probs, label="Game 2 Probability")
plt.axvline(x=0.5, color='red', linestyle='--', label="Intersection (~0.5)")
plt.xlabel("Probability of Making a Shot (p)")
plt.ylabel("Winning Probability")
plt.title("Comparison of Winning Probabilities for Game 1 and Game 2")
plt.legend()
plt.grid()
plt.show()

# Determine for which values of p to choose each game
for p in [0.1, 0.3, 0.5, 0.7, 0.9]:
    g1 = game1_probability(p)
    g2 = game2_probability(p)
    if g1 > g2:
        print(f"For p = {p:.2f}, choose Game 1 (P1: {g1:.3f}, P2: {g2:.3f})")
    else:
        print(f"For p = {p:.2f}, choose Game 2 (P1: {g1:.3f}, P2: {g2:.3f})")

Result Graph

Dominos

There is an 8x8 chessboard in which two diagonally opposite corners have been cut off. You are given 31 dominos, and a single domino can cover exactly two squares. Can you use the 31 dominos to cover the entire board? Prove your answer (by providing an example or showing why it's impossible)

Approach

Domino covers exactly 2 squares that are adjacent to each other. And chessboard squares are different colors (Black and White)
So, when Domino cover exactly two squares, It will always cover one black and one while
Therefore, the number of black squares and white squares must be equal
However, Every chessboard always the same color in the diagonally opposite corners
Thus, It is impossible

Python

  
def can_cover_with_dominos():
    board = [[(i + j) % 2 for j in range(8)] for i in range(8)]
    # Delete two diagonally opposite corners
    board[0][0] = -1
    board[7][7] = -1
    
    black_count = sum(cell == 1 for row in board for cell in row)
    white_count = sum(cell == 0 for row in board for cell in row)
    
    print("Black squares:", black_count)
    print("White squares:", white_count)
    
    if black_count != white_count:
        return "Impossible to cover the board with 31 dominos."
    else:
        return "Possible to cover the board with 31 dominos."

print(can_cover_with_dominos())

Proof: The opposite corners of an N * N chessboard have the same color
- Example
  If (i + j) is even == white
  If (i + j) is odd == black
  And (0, 0) is even == white
- So, The bottom-right corner is
  (N - 1) + (N - 1) = 2N - 2 == Always even

100 Lockers

There are 100 closed lockers in a hallway. A man begins by opening all 100 lockers. Next, he closes every second locker.
Then, on his third pass, he toggles every third locker (closes it if it is open or opens it if it is closed).
This process continues for 100 passes, such that on each pass i, the man toggles every ith locker. After his 100th pass in the hallway, in which he toggles only locker #100, how many lockers are open?

Approach

For example, scenario with 6 lockers (not a 100)

  O : open , C : close

  1 2 3 4 5 6
  O O O O O O
    C   C   C
      C     O
        O
          C
            C

Only 1, 4 locker is opened

Odd number of divisors (1, 4, 9, …) == Locker is always closed
2 of divisor : 1, 2 (even) == Locker is closed
6 of divisor : 1, 2, 3, 6 (even) == Locker is closed
Thus, only lockers numbered as perfect squares will remain open

Python

  
def countOpenLockers(n):
    return int(n**0.5)

# Ask the number of lockers
try:
    n = int(input("Number of lockers : "))
    if n <= 0:
        print("Only positive integer")
    else:
        result = countOpenLockers(n)
        print(f"Number of openv lockers for {n} lockers : {result}")
except ValueError:
    print("Invalid Input")

Posion

You have 1000 bottles of soda, and exactly one is poisoned. You have 10 test strips which can be used to detect poison. A single drop of poison will turn the test strip positive permanently.
You can put any number of drops on a test strip at once and you can reuse a test strip as many time as you’d like (as long as the results are negative).
However, you can only run tests once per day and it takes seven days to return a result. How would you figure out the poisoned bottle in as few days as possible?

Approach

Since binary is 0, 1, it can also be interpreted as True, False. Therefore, converting numbers (0 ~ 1000) into binary.
A 10-bit binary number can represent up to 1024, so the range is sufficient. Now, think of each binary digit as a test strip
bit == The place where I can use test strip
If the digit is 1, using the test strip. Even if non-poison drinks continuously tested, the result will remain negative
However, negative test strip encounters a poison soda, the result will react positively
Test all 1000 drinks with the test strips in one day and wait 7 days after the result
If the result is negative -> converting 0
Result is positive -> 1
Convert this binary -> Convert 10-base again -> This bottle is poison

Python

  
import random

def findPoisonBottle(numBottles=1000, numStrips=10):
    poisonedBottle = random.randint(1, numBottles)
    bottles = list(range(1, numBottles + 1))
    binaryList = [format(bottle, f'0{numStrips}b') for bottle in bottles]
    results = [0] * numStrips

    for i in range(numStrips):
        if format(poisonedBottle, f'0{numStrips}b')[i] == '1':
            results[i] = 1

    print(f"Simulated test strip results: {results}")
    detectedBinary = ''.join(map(str, results))
    detectedPoisonedBottle = int(detectedBinary, 2)
    
    if detectedPoisonedBottle == poisonedBottle:
        return detectedPoisonedBottle
    else:
        return f"Error: Detected bottle ({detectedPoisonedBottle}) does not match the actual poisoned bottle ({poisonedBottle})."

detectedBottle = findPoisonBottle()
print(f"The poisoned bottle detected by the algorithm is: {detectedBottle}")

Result

Simulated test strip results: [1, 1, 1, 0, 0, 0, 1, 0, 0, 1]
The poisoned bottle detected by the algorithm is: 905

format(bottle, f'010b') : Convert a decimal number (bottle) into a binary

  binaryList = [format(bottle, f'0{numStrips}b') for bottle in bottles]
                                 0 : padding with zeros
                                   numStrips (10) : 10 characters
                                             b : binary

  
  print(format(5, '8b'))    # 8 characters, padded with spaces: "     101"
  print(format(5, '08b'))   # 8 characters, padded with zeros: "00000101"

List Comprehension

  
  binaryList = [format(bottle, f'0{numStrips}b') for bottle in bottles]

More intuitive and easier

Using lambda with map()
1 binaryList = list(map(lambda bottle : format(bottle, f'0{numStrips}b', bottles)))
Simple, But it is hard to notice what it is
So, lambda is called : anonymous function

Java

  
import java.util.Random;

public class PoisonBottle {
    public static void main(String[] args) {
        int numBottles = 1000;
        int numStrips = 10;

        int poisonedBottle = new Random().nextInt(numBottles) + 1;
        String[] binaryList = new String[numBottles];
        int[] results = new int[numStrips];

        for (int i = 0; i < numBottles; i++) {
            binaryList[i] = String.format("%" + numStrips + "s", Integer.toBinaryString(i + 1)).replace(' ', '0');
        }

        String poisonedBinary = String.format("%" + numStrips + "s", Integer.toBinaryString(poisonedBottle)).replace(' ', '0');
        for (int i = 0; i < numStrips; i++) {
            if (poisonedBinary.charAt(i) == '1') {
                results[i] = 1;
            }
        }

        System.out.println("Simulated test strip results:");
        for (int result : results) {
            System.out.print(result);
        }
        System.out.println();

        StringBuilder detectedBinary = new StringBuilder();
        for (int result : results) {
            detectedBinary.append(result);
        }
        int detectedPoisonedBottle = Integer.parseInt(detectedBinary.toString(), 2);

        if (detectedPoisonedBottle == poisonedBottle) {
            System.out.println("The poisoned bottle detected by the algorithm is: " + detectedPoisonedBottle);
        } else {
            System.out.println("Error: Detected bottle (" + detectedPoisonedBottle + ") does not match the actual poisoned bottle (" + poisonedBottle + ").");
        }
    }
}

int poisonedBottle = new Random().nextInt(numBottles) + 1;
Since the object is not stored in a variable, this Random object cannot be reused after the method call
Therefore, the Random object is temporarily created in memory, and once its use is complete, it is cleaned up by the Garbage Collector (GC)
Java : binaryList[i] = String.format("%" + numStrips + "s", Integer.toBinaryString(i + 1)).replace(' ', '0');
== Python : binaryList = [format(bottle, f'0{numStrips}b') for bottle in bottles]
- "%" + numStrips + "s" : the fixed width of numStrips(10)
StringBuilder detectedBinary = new StringBuilder();
Unlike String class, StringBuilder is mutable, meaing it allows modifications to string

C++

  
#include <iostream>
#include <bitset>
#include <cstdlib>
#include <ctime>
#include <string>

int main() {
    const int numBottles = 1000;
    const int numStrips = 10;

    srand(time(0));
    int poisonedBottle = rand() % numBottles + 1;
    int results[numStrips] = {0};

    std::string poisonedBinary = std::bitset<10>(poisonedBottle).to_string();
    for (int i = 0; i < numStrips; i++) {
        if (poisonedBinary[i] == '1') {
            results[i] = 1;
        }
    }

    std::cout << "Simulated test strip results: ";
    for (int i = 0; i < numStrips; i++) {
        std::cout << results[i];
    }
    std::cout << std::endl;

    std::string detectedBinary = "";
    for (int i = 0; i < numStrips; i++) {
        detectedBinary += std::to_string(results[i]);
    }
    int detectedPoisonedBottle = std::stoi(detectedBinary, nullptr, 2);

    if (detectedPoisonedBottle == poisonedBottle) {
        std::cout << "The poisoned bottle detected by the algorithm is: " << detectedPoisonedBottle << std::endl;
    } else {
        std::cout << "Error: Detected bottle (" << detectedPoisonedBottle << ") does not match the actual poisoned bottle (" << poisonedBottle << ")." << std::endl;
    }

    return 0;
}

srand(time(0))
time(0) : Return the current time in seconds
So, the random numbers is generated every time the program is executed because time is always change

Go

  
package main

import (
	"fmt"
	"math/rand"
	"strconv"
	"time"
)

func main() {
	rand.Seed(time.Now().UnixNano())
	numBottles := 1000
	numStrips := 10

	poisonedBottle := rand.Intn(numBottles) + 1
	results := make([]int, numStrips)

	poisonedBinary := fmt.Sprintf("%0*b", numStrips, poisonedBottle)
	for i := 0; i < numStrips; i++ {
		if poisonedBinary[i] == '1' {
			results[i] = 1
		}
	}
	fmt.Printf("Simulated test strip results: %v\n", results)

	detectedBinary := ""
	for _, result := range results {
		detectedBinary += strconv.Itoa(result)
	}
	detectedPoisonedBottle, _ := strconv.ParseInt(detectedBinary, 2, 64)

	if int(detectedPoisonedBottle) == poisonedBottle {
		fmt.Printf("The poisoned bottle detected by the algorithm is: %d\n", detectedPoisonedBottle)
	} else {
		fmt.Printf("Error: Detected bottle (%d) does not match the actual poisoned bottle (%d).\n", detectedPoisonedBottle, poisonedBottle)
	}
}

rand.Seed(time.Now().UnixNano())
rand generates pseudo-random numbers, and return the current time as a nanosecond timestamp
C++ : int results[numStrips] = {0}; == Go : results := make([]int, numStrips)
make : create a slice of int with length of numStrips
All elements initialized to default value 0
%0*b format specifier : padding with 0
== C++ : std::string poisonedBinary = std::bitset<10>(poisonedBottle).to_string();
== Java : String poisonedBinary = String.format("%" + numStrips + "s", Integer.toBinaryString(poisonedBottle)).replace(' ', '0');

CrackingCoding

This post is licensed under CC BY 4.0 by the author.

Basketball

Approach

Prerequisite

Python

Dominos

Approach

Python

100 Lockers

Approach

Python

Posion

Approach

Python

Java

C++

Go

Trending Tags