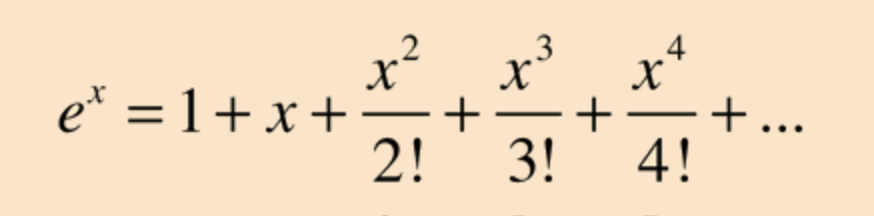[LeetCode] Recursion, Linked Lists, and Taylor Series in Python and C++

Prepare to PCCP exam

Code : LeetCode

1. sorted(arr) VS arr.sort()

• If you need a sorted copy of the list while keeping the original list → sorted(arr)

• If you want to sort the original list itself → arr.sorted()

Recursion

1. Code

void fun1(int n)
{
	if (n > 0)
	{
		printf("%d\n", n);
		fun1(n-1);
	}
}

void main()
{
	int x = 3;
	fun1(x);
}

• Output : 3 2 1 (printing → calling itself)

1. Code

void fun2(int n)
{
	if (n > 0)
	{
		fun2(n -1);
		printf("%d\n", n);
	}
}

void main()
{
	int x = 3;
	fun2(x);
}

• Output : 1 2 3 (calling itself → printing)

Linked List

• While lists use a contiguous memory block to store references to their data, linked lists store references as part of their own elements.

• references and pointer mean essentially the same thing

  It’s the memory address of the next node, allowing the list to know where to find each subsequent node

1. Code

#Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        cur = dummy = ListNode()

        while list1 and list2:
            if list1.val < list2.val:
                cur.next = list1
                list1, cur = list1.next, list1
            else:
                cur.next = list2
                list2, cur = list2.next, list2
        

        if list1 or list2:
            cur.next = list1 if list1 else list2
        
        return dummy.next

Taylor Series

• Evaluating a Taylor Series for n times then total multiplication

  2 * (n(n+1)/2) → Time Complexity : O(n^2)

• However, we can reduce the multiplications to reduce Tinme Complexity

  For example, e^4 = 1 + x/1[1 + x/2[1 + x/3[1 + x/4]]]

  So, the total multiplication is O(n)

1. Code

double e(int x, int n)
{
	static double s;
	
	if (n==0)
		return s;

	s = 1 + x*(s/n);
	return e(x, n-1);
}
int main()
{
	printf("%lf\n", e(1,10));
	return 0;
}

• Output : e^1 (However, It is not 100% accurate)

  If you want more accurate value, then increase the value 10 to 15 or 20 etc.